Problem 48
Five people stand at the vertices of a pentagon, throwing frisbees to each other.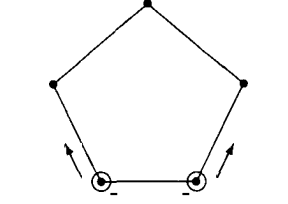
They have two frisbees, initially at adjacent vertices as shown. In each time interval, each frisbee is thrown either to the left or to the right (along an edge of the pentagon) with equal probability. This process continues until one person is the target of two frisbees simultaneously; then the game stops. (All throws are independent of past history.)
- a) Find the mean and variance of the number of pairs of throws.
- b) Find a closed form for the probability that the game lasts more than 100 steps, in terms of Fibonacci numbers.
solution
Based on the relative distance between frisbee, there are three states, that is state C (d=1), state B (d=2) and state A (d=0).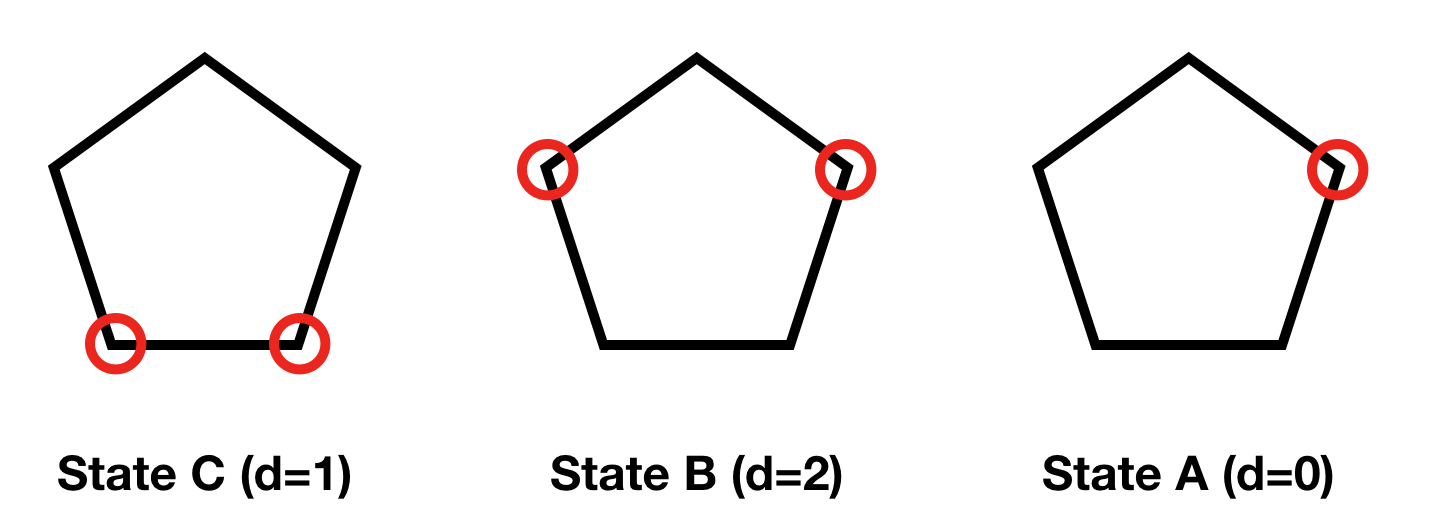
And the transition among states is shown below: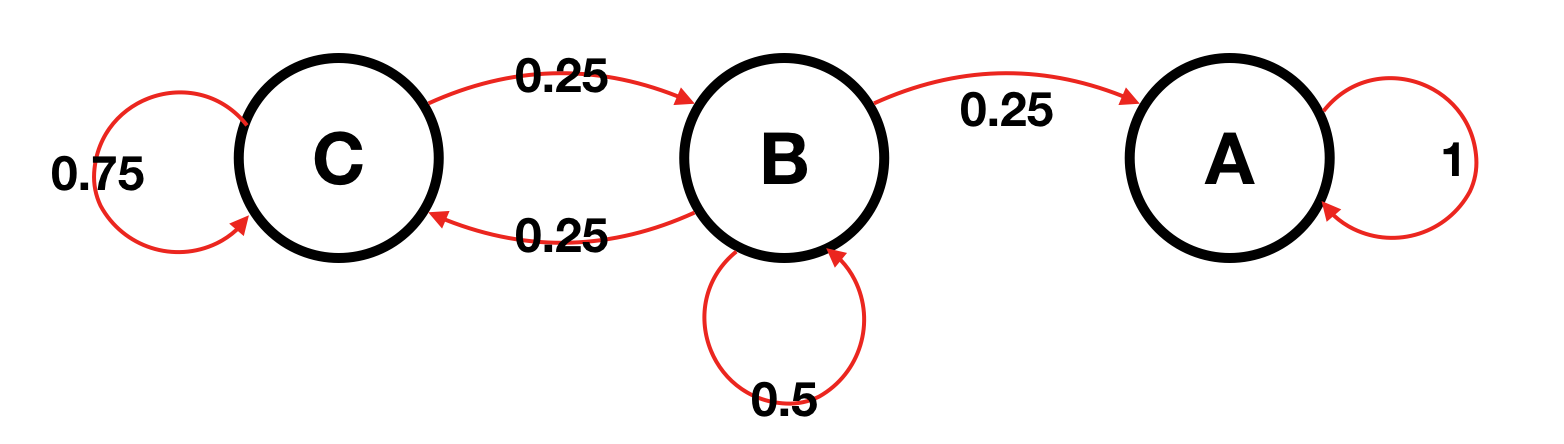
so the transition matrix $T = \begin{bmatrix}
& A_{n-1} & B_{n-1} & C_{n-1} \\\\
A_n & 1 & 1/4 & 0 \\\\
B_n & 0 & 1/2 & 1/4 \\\\
C_n & 0 & 1/4 & 3/4
\end{bmatrix}$, and initial state vector $P(0)=\begin{bmatrix}
0 \\\\
0 \\\\
1
\end{bmatrix}$.
During round n, $P(n)=T^n P(0)$, and $p(n)=P(n) - P(n-1)=T^{n-1}(T-I)P(0)$.
We need to calculate $E(n)$ and $D(n)$. where
$$\begin{bmatrix}
E_a(n) \\\\
E_b(n) \\\\
E_c(n)
\end{bmatrix} = E(n) = \sum_{n=1}^{\infty} n p(n)$$
$$D(n) = E(n^2) - E(n)^2 = \sum_{n=1}^{\infty} n^2 p(n) - E(n)^2$$
First we need to compute Jordan Canonical Form of $T$, $VJV^{-1}=T$.
$V=\begin{bmatrix}
0 & \frac{\sqrt 5-1}{2} & -\frac{\sqrt 5+1}{2} \\\\
0 & -\frac{\sqrt 5+1}{2} & \frac{\sqrt 5-1}{2} \\\\
0 & 1 & 1
\end{bmatrix}, J=\begin{bmatrix}
1 & & \\\\
& \frac{5 - \sqrt 5}{8} & \\\\
& & \frac{5 + \sqrt 5}{8}
\end{bmatrix}$
$E(n)$
$ = \sum_{n=1}^{\infty} n p(n) = \sum_{n=1}^{\infty} n T^{n-1} (T - I) P(0) $
$= \sum_{n=1}^{\infty} n V J^n V^{-1} (T-I)P(0)=V \left( \sum_{n=1}^{\infty} n J^n \right )V^{-1} (T-I) P(0)$
$=V \begin{bmatrix}
\sum_{n=1}^{\infty} n & & \\\\
& \sum_{n=1}^{\infty} n (\frac{5-\sqrt 5}{8})^n & \\\\
& & \sum_{n=1}^{\infty} n (\frac{5+\sqrt 5}{8})^n
\end{bmatrix} V^{-1} (T-I) P(0)$
$=V \begin{bmatrix}
\infty & & \\\\
& \frac{1}{(1 - \frac{5-\sqrt 5}{8})^2} & \\\\
& & \frac{1}{(1 - \frac{5+\sqrt 5}{8})^2}
\end{bmatrix} V^{-1} (T-I) P(0)$
$=V \begin{bmatrix}
\infty & & \\\\
& \frac{1}{(1 - \frac{5-\sqrt 5}{8})^2} & \\\\
& & \frac{1}{(1 - \frac{5+\sqrt 5}{8})^2}
\end{bmatrix} V^{-1} (T-I) P(0) = \begin{bmatrix}
12 \\\\ -4 \\\\ -8 \end{bmatrix}$
where $E_a(n) = 12$.
And $E_a(n^2)=244$ is computed in the same way, we skip the procedure.
$D_a(n) = E_a(n^2) - E_a(n)^2 = 244 - 12^2 = 100$.