representation
Graphical Model = graph theory + probabilistic theory
- directed: bayesian network
- undirected: Markov network
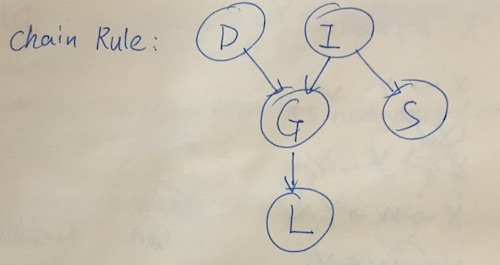
Chain rule representation:
\( P(D,I,G,L,S)=\prod_i P(i|Par(i)) = P(L|G)\cdot P(G|I,D)\cdot P(D)\cdot P(I) \cdot P(S|I) \)
Factors are building blocks for defining distributions in high dimensional space
Reasoning: Casual reasoning, Evidence reasoning, Intercausal reasoning
Can X influence Y?
\( X \leftarrow Y \checkmark \)
\( X \rightarrow Y \checkmark \)
\( X \rightarrow W \rightarrow Y \checkmark \)
\( X \leftarrow W \leftarrow Y \checkmark \)
\( X \leftarrow W \rightarrow Y \checkmark \)
\( X \rightarrow W \leftarrow Y \times \) V structure
Can X influence Y given Z?
\( X \leftarrow Y \checkmark \)
\( X \rightarrow Y \checkmark \)
\( X \rightarrow W \rightarrow Y (W\in Z \checkmark) (W \notin Z \times) \)
\( X \leftarrow W \leftarrow Y (W \in Z \checkmark) (W \notin Z \times) \)
\( X \leftarrow W \rightarrow Y (W \in Z \checkmark) (W \notin Z \times) \)
\( X \rightarrow W \leftarrow Y (W \in Z \times) (W \notin Z \checkmark) \)
W and its children are not observed.
independence
\( P \models \alpha \perp \beta \rightarrow P(\alpha,\beta)=P(\alpha)P(\beta) \)
\( \models\) means satisfy, \(\perp\) means independent.
Conditional independence \( P(X,Y|Z)=P(X|Z)P(Y|Z)\rightarrow P \models (X \perp Y|Z) \)
\( P(X|Y,Z)=P(X|Z) \)
Relationship between independence and factorization \( P(X,Y,Z) \propto \phi(X,Z)\cdot\phi(Y,Z) \)
D-sep
No active trail in G between X and Y given Z. d-sep(X,Y|Z).
Theorem: if P factorize over G, and d-sep(X,Y|Z) then \( P \models (X\perp Y|Z) \).
Any node is d-sep from its non-descendants given its parents.
View of graph structure:
- factorization;
- I-map: independence encoded by G hold in P.
\( I(G)={(X\perp Y|Z):dsep(X,Y|Z)} \)
If \( P \models I(G) \), then G is independency map of P.
Theorem: If P factorize over G, then G is I-map for P.
Naive bayes model

assumption: \( (X_i \perp X_j | C) \).
robot localization
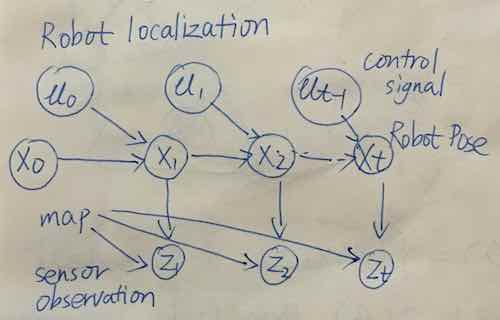
Template model
Template variable is instantiated multiple times.
Markov assumption:
\( P(X^{0:T})=P(X^0)\prod_{t=0}^T P(X^{t+1}|X^t) \).
\( (X^{t+1} \perp X^{0:t-1}|X^t) \)
Table CPD is problemetic, it has \( 2^n \) growth of parents.
Template model has parameter sharing structure.
CRF
Conditional Random Field
\( Z(X)=\sum_{Y} P_{\phi}(X,Y), P(Y|X)= \frac{1}{Z(X)}P_{\phi}(X,Y) \)
When features are correlated, we need to compute P(Y|X) instead of P(X,Y).
Let \( \Phi={\phi_1(D_1),…,\phi_k(D_k)} \),
\( Z_{/phi}=\sum_Y \tilde{P}_{\phi}(X,Y) \),
\( \tilde{P}(Y|X)=\frac{1}{Z_{\phi}}\tilde{P_{\phi}}(X,Y) \)
Logistic regression model
logistic regression is discriminate model, no independence assumption, correlations don’t matter.
\( \phi_{i}(X_i,Y=1)=e^{w_i x_i} \)
\( \phi_{i}(X_i,Y=0)=e^0=1 \)
\( \tilde{P_{\Phi}}(X,Y=1)=\prod_i e^{w_i x_i}=e^{\sum_i w_i x_i} \)
\( \tilde{P_{\Phi}}(X,Y=0)=1 \)
$$ P(Y=1|X)=\frac{P(Y=1,X)}{P(Y=1,X)+P(Y=0,X)}=\frac{e^{\sum_{i}w_i x_i}}{e^{\sum_i w_i x_i}+1} $$
If P factorize over H, and \( Sep_H(X,Y|Z), P \models (X\perp Y |Z) \)
Minimum I-map, Perfect I-map, I-equivalence: \(G_1,G_2\) over \(X_1,…,X_n\) are equivalent, if \(I(G_1)=I(G_2)\).
Decison Making
actions: \(Val(A)={a^1,…,a^k} \);
states: \(Val(X)={x^1,…,x^k} \);
Utility function: U(X,A)
Expected Utility \( EU(D(a))=\sum_X P(X|a)U(X|a) \)
\( a^*=argmax_a EU(D(a)) \)
Value of Information: \( VPI(A|X)=MEU(D_{x\rightarrow A})-MEU(D) \)
Pairwise Markov Network
Node: \( x_i,…,x_j \);
Edge: \(\phi_{ij}(x_i,x_j) \)
Partition function: \( P(x_1,x_2)=\frac{1}{Z}\phi_1\phi_2 \).
demerits: pairwise markov network is not very expressive: \( O(n^2d^2) \) parameters, while bayesian network has \( O(d^n) \) parameters.
Active trail in markov network: no block in \( x_i,…,x_n\) trail.